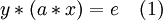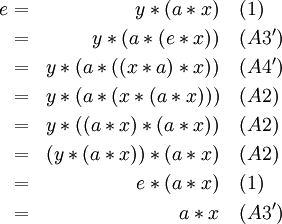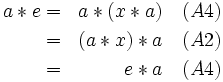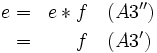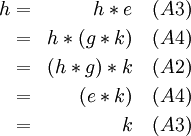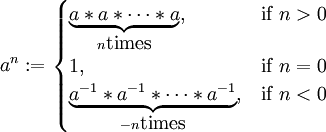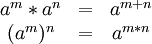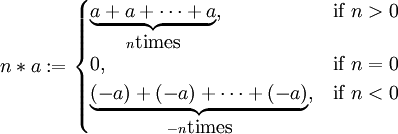Elementary group theory
2008/9 Schools Wikipedia Selection. Related subjects: Mathematics
In mathematics, a group ⟨G,*⟩ is defined as a set G and a binary operation on G, called product and denoted by infix "*". Product obeys the following rules (also called axioms). Let a, b, and c be arbitrary elements of G. Then:
- A1, Closure. a*b is in G;
- A2, Associativity. (a*b)*c=a*(b*c);
- A3, Identity. There exists an identity element e in G such that a*e=e*a=a. e, the identity of G, is unique by Theorem 1.4 below;
- A4, Inverse. For each a in G, there exists an inverse element x in G such that a*x=x*a=e. x, the inverse of a, is unique by Theorem 1.5 below.
An abelian group also obeys the additional rule:
- A5, Commutativity. a*b = b*a.
Closure is part of the definition of "binary operation," so that A1 is often omitted.
Elaboration
- Group product "*" is not necessarily multiplication. Addition works just as well, as do many less standard operations.
- When * is a standard operation, we use the standard symbol instead (for example, + for addition).
- When * is addition or any commutative operation (except multiplication), 0 usually denotes the identity and -a denotes the inverse of a. The operation is always denoted by something other than * -- often + -- to avoid confusion with multiplication.
- When * is multiplication or a noncommutative operation,a*b is often written ab. 1 usually denotes the identity element, and a -1 usually denotes the inverse of a.
- The group ⟨G,*⟩ is often referred to as "the group G" or simply "G"; but the operation "*" is fundamental to the description of the group.
- ⟨G,*⟩ is usually pronounced "the group G under *". When affirming that G is a group (for example, in a theorem), we say that "G is a group under *".
Examples
G={1,-1} is a group under multiplication, because for all elements a, b, c in G:
- A1: a*b is an element of G.
- A2: (a*b)*c=a*(b*c) can be verified by enumerating all 8 possible (and trivial) cases.
- A3: a*1=a. Hence 1 is an identity element.
- A4: a-1*a=1. Hence a-1 denotes inverse and 1 is an inverse element.
- A2: (a*b)*c=a*(b*c) can be verified by enumerating all 8 possible (and trivial) cases.
The integers Z and the real numbers R are groups under addition '+'. For all elements a, b, and c of either Z or R:
- A1: Adding any two numbers yields another number of the same kind.
- A2: (a+b)+c=a+(b+c).
- A3: a+0=a. Hence 0 is an identity element.
- A4: -a+a=0. Hence -a denotes inverse and 0 is an inverse element.
- A2: (a+b)+c=a+(b+c).
The real numbers R are NOT a group under multiplication '*'. For all a, b, and c in R:
- A3: 1.
- A4: 0*a=0, so 0 has no inverse.
The real numbers without 0, R#, are a group under multiplication '*'.
- A1: Multiplying any two elements of R# yields another element of R#.
- A2: (a*b)*c=a*(b*c).
- A3: a*1=a. Hence 1 denotes identity.
- A4: a -1*a=1. Hence a -1 denotes inverse.
- A2: (a*b)*c=a*(b*c).
Alternative Axioms
A3 and A4 can be replaced by:
- A3’, left neutral. There exists an e in G such that for all a in G, e*a=a.
- A4’, left inverse. For each a in G, there exists an element x in G such that x*a=e.
Or alternatively by:
- A3’’, right neutral. There exists an e in G such that for all a in G, a*e=a.
- A4’’, right inverse. For each a in G, there exists an element x in G such that a*x=e.
These apparently weaker pairs of axioms are naturally implied by A3 and A4. We will now show that the converse is true.
Theorem: Assuming A1 and A2, A3’ and A4’ imply A3 and A4.
Proof. Let a left neutral element e be given, and a in G. By A4’ there exist an x such that a*x=e. We show that also x*a**=e. Per A4’ there is an y in G with:
Therefore:
This establishes A4.
This establishes A3.
Theorem: Assuming A1 and A2, A3’’ and A4’’ imply A3 and A4.
Proof. Similar to the above.
Basic theorems
Identity is unique
Theorem 1.4: The identity element of a group ⟨G,*⟩ is unique.
Proof: Suppose that e and f are two identity elements of G. Then
As a result, we can speak of the identity element of ⟨G,*⟩ rather than an identity element. Where different groups are being discussed and compared, eG denotes the identity of the specific group ⟨G,*⟩.
Inverses are unique
Theorem 1.5: The inverse of each element in ⟨G,*⟩ is unique.
Proof: Suppose that h and k are two inverses of an element g of G. Then
As a result, we can speak of the inverse of an element a, rather than an inverse. Without ambiguity, for all a in G, we denote by a -1 the unique inverse of a.
Latin square property
Theorem 1.3: For all elements a,b in G, there exists a unique x in G such that a*x = b.
Proof. At least one such x surely exists, for if we let x = a -1*b, then x is in G (by A1, closure) and:
- a*x = a*(a -1*b) (substituting for x)
- a*(a -1*b) = (a*a -1)*b (associativity A2).
- (a*a -1)*b= e*b = b. (identity A3).
- Thus an x always exists satisfying a*x = b.
To show that this is unique, if a*x=b, then
- x = e*x
- e*x = (a -1*a)*x
- (a -1*a)*x = a -1*(a*x)
- a -1*(a*x) = a -1*b
- Thus, x = a -1*b
Similarly, for all a,b in G, there exists a unique y in G such that y*a = b.
Inverting twice gets you back where you started
Theorem 1.6: For all elements a in group G, (a -1) -1=a.
Proof. a -1*a = e. The conclusion follows from Theorem 1.4.
Inverse of ab
Theorem 1.7: For all elements a,b in group G, (a*b) -1=b -1*a -1.
Proof. (a*b)*(b -1*a -1) = a*(b*b -1)*a -1 = a*e*a -1 = a*a -1 = e. The conclusion follows from Theorem 1.4.
Cancellation
Theorem 1.8: For all elements a,x, and y in group G, if a*x=a*y, then x=y; and if x*a=y*a, then x=y.
Proof. If a*x = a*y then:
- a -1*(a*x) = a -1*(a*y)
- (a -1*a)*x = (a -1*a)*y
- e*x = e*y
- x = y
If x*a = y*a then
- (x*a)*a -1 = (y*a)*a -1
- x*(a*a -1) = y*(a*a -1)
- x*e = y*e
- x = y
Powers
For 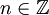 and
and 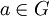 we define:
we define:
Theorem 1.9: For all a in group ⟨G,*⟩, 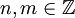 :
:
Similarly if G is written in additive notation, we have:
and:
Order
Of a group element
The order of an element a in a group G is the least positive integer n such that an = e. Sometimes this is written "o(a)=n". n can be infinite.
Theorem 1.10: A group whose nontrivial elements all have order 2 is abelian. In other words, if all elements g in a group G g*g=e is the case, then for all elements a,b in G, a*b=b*a.
Proof. Let a, h be any 2 elements in the group G. By A1, a*h is also a member of G. Using the given condition, we know that (a*h)*(a*h)=e. Hence:
- a*(a*b)*(a*b) = a*e
- a*(a*b)*(a*b)*b = a*e*b
- (a*a)*(b*a)*(b*b) = (a*e)*b
- e*(b*a)*e = a*b
- b*a = a*b.
Since the group operation * commutes, the group is abelian
Of a group
The order of the group G, usually denoted by |G| or occasionally by o(G), is the number of elements in the set G, in which case ⟨G,*⟩ is a finite group. If G is an infinite set, then the group ⟨G,*⟩ has order equal to the cardinality of G, and is an infinite group.
Subgroups
A subset H of G is called a subgroup of a group ⟨G,*⟩ if H satisfies the axioms of a group, using the same operator "*", and restricted to the subset H. Thus if H is a subgroup of ⟨G,*⟩, then ⟨H,*⟩ is also a group, and obeys the above theorems, restricted to H. The order of subgroup H is the number of elements in H.
A proper subgroup of a group G is a subgroup which is not identical to G. A non-trivial subgroup of G is (usually) any proper subgroup of G which contains an element other than e.
Theorem 2.1: If H is a subgroup of ⟨G,*⟩, then the identity eH in H is identical to the identity e in (G,*).
Proof. If h is in H, then h*eH = h; since h must also be in G, h*e = h; so by theorem 1.4, eH = e.
Theorem 2.2: If H is a subgroup of G, and h is an element of H, then the inverse of h in H is identical to the inverse of h in G.
Proof. Let h and k be elements of H, such that h*k = e; since h must also be in G, h*h -1 = e; so by theorem 1.5, k = h -1.
Given a subset S of G, we often want to determine whether or not S is also a subgroup of G. A handy theorem valid for both infinite and finite groups is:
Theorem 2.3: If S is a non-empty subset of G, then S is a subgroup of G if and only if for all a,b in S, a*b -1 is in S.
Proof. If for all a, b in S, a*b -1 is in S, then
- e is in S, since a*a -1 = e is in S.
- for all a in S, e*a -1 = a -1 is in S
- for all a, b in S, a*b = a*(b -1) -1 is in S
Thus, the axioms of closure, identity, and inverses are satisfied, and associativity is inherited; so S is subgroup.
Conversely, if S is a subgroup of G, then it obeys the axioms of a group.
- As noted above, the identity in S is identical to the identity e in G.
- By A4, for all b in S, b -1 is in S
- By A1, a*b -1 is in S.
The intersection of two or more subgroups is again a subgroup.
Theorem 2.4: The intersection of any non-empty set of subgroups of a group G is a subgroup.
Proof. Let {Hi} be a set of subgroups of G, and let K = ∩{Hi}. e is a member of every Hi by theorem 2.1; so K is not empty. If h and k are elements of K, then for all i,
- h and k are in Hi.
- By the previous theorem, h*k -1 is in Hi
- Therefore, h*k -1 is in ∩{Hi}.
Therefore for all h, k in K, h*k -1 is in K. Then by the previous theorem, K=∩{Hi} is a subgroup of G; and in fact K is a subgroup of each Hi.
Given a group ⟨G,*⟩, define x*x as x², x*x*x*...*x (n times) as xn, and define x0 = e. Similarly, let x -n for (x -1)n. Then we have:
Theorem 2.5: Let a be an element of a group (G,*). Then the set {an: n is an integer} is a subgroup of G.
Proof. A subgroup of this type is called a cyclic subgroup; the subgroup of the powers of a is often written as <a>, and we say that a generates <a>.
Cosets
If S and T are subsets of G, and a is an element of G, we write "a*S" to refer to the subset of G made up of all elements of the form a*s, where s is an element of S; similarly, we write "S*a" to indicate the set of elements of the form s*a. We write S*T for the subset of G made up of elements of the form s*t, where s is an element of S and t is an element of T.
If H is a subgroup of G, then a left coset of H is a set of the form a*H, for some a in G. A right coset is a subset of the form H*a.
If H is a subgroup of G, the following useful theorems, stated without proof, hold for all cosets:
- And x and y are elements of G, then either x*H = y*H, or x*H and y*H have empty intersection.
- Every left (right) coset of H in G contains the same number of elements.
- G is the disjoint union of the left (right) cosets of H.
- Then the number of distinct left cosets of H equals the number of distinct right cosets of H.
Define the index of a subgroup H of a group G (written "[G:H]") to be the number of distinct left cosets of H in G.
From these theorems, we can deduce the important Lagrange's theorem, relating the order of a subgroup to the order of a group:
- Lagrange's theorem: If H is a subgroup of G, then |G| = |H|*[G:H].
For finite groups, this can be restated as:
- Lagrange's theorem: If H is a subgroup of a finite group G, then the order of H divides the order of G.
- If the order of group G is a prime number, G is cyclic.