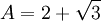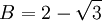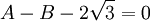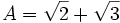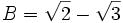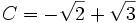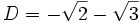Galois theory

2008/9 Schools Wikipedia Selection. Related subjects: Mathematics

In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory. Using Galois theory, certain problems in field theory can be reduced to group theory, which is in some sense simpler and better understood.

Originally Galois used permutation groups to describe how the various roots of a given polynomial equation are related to each other. The modern approach to Galois theory, developed by Richard Dedekind, Leopold Kronecker and Emil Artin, among others, involves studying automorphisms of field extensions.

Further abstraction of Galois theory is achieved by the theory of Galois connections.

Application to classical problems

The birth of Galois theory was originally motivated by the following question, which is known as the Abel-Ruffini theorem.

"Why is there no formula for the roots of a fifth (or higher) degree polynomial equation in terms of the coefficients of the polynomial, using only the usual algebraic operations (addition, subtraction, multiplication, division) and application of radicals (square roots, cube roots, etc)?"

Galois theory not only provides a beautiful answer to this question, it also explains in detail why it is possible to solve equations of degree four or lower in the above manner, and why their solutions take the form that they do.

Galois theory also gives a clear insight into questions concerning problems in compass and straightedge construction. It gives an elegant characterisation of the ratios of lengths that can be constructed with this method. Using this, it becomes relatively easy to answer such classical problems of geometry as

"Which regular polygons are constructible polygons?"

"Why is it not possible to trisect every angle?"

The permutation group approach to Galois theory

If we are given a polynomial, it may happen that some of the roots of the polynomial are connected by various algebraic equations. For example, it may turn out that for two of the roots, say A and B, the equation A² + 5B³ = 7 holds. The central idea of Galois theory is to consider those permutations (or rearrangements) of the roots having the property that any algebraic equation satisfied by the roots is still satisfied after the roots have been permuted. An important proviso is that we restrict ourselves to algebraic equations whose coefficients are rational numbers. (One might instead specify a certain field in which the coefficients should lie, but for the simple examples below, we will restrict ourselves to the field of rational numbers.)

These permutations together form a permutation group, also called the Galois group of the polynomial (over the rational numbers). This can be made much clearer by way of example.

First example — a quadratic equation

Consider the quadratic equation

x² − 4x + 1 = 0.

By using the quadratic formula, we find that the two roots are

Examples of algebraic equations satisfied by A and B include

A + B = 4,   and

AB = 1.

Obviously, in either of these equations, if we exchange A and B, we obtain another true statement. For example, the equation A + B = 4 becomes simply B + A = 4. Furthermore, it is true, but far less obvious, that this holds for every possible algebraic equation with rational coefficients satisfied by A and B; to prove this requires the theory of symmetric polynomials.

We conclude that the Galois group of the polynomial x² − 4x + 1 consists of two permutations: the identity permutation which leaves A and B untouched, and the transposition permutation which exchanges A and B. It is a cyclic group of order two, and therefore isomorphic to Z/2Z.

One might raise the objection that A and B are related by yet another algebraic equation,

which does not remain true when A and B are exchanged. However, this equation does not concern us, because it does not have rational coefficients; in particular, 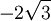is not rational.

A similar discussion applies to any quadratic polynomial ax² + bx + c, where a, b and c are rational numbers.

• If the polynomial has only one root, for example x² − 4x + 4 = (x−2)², then the Galois group is trivial; that is, it contains only the identity permutation.
• If it has two distinct rational roots, for example x² − 3x + 2 = (x−2)(x−1), the Galois group is again trivial.
• If it has two irrational roots (including the case where the roots are complex), then the Galois group contains two permutations, just as in the above example.

Second example — somewhat trickier

Consider the polynomial

x⁴ − 10x² + 1,

which can also be written as

(x² − 5)² − 24.

We wish to describe the Galois group of this polynomial, again over the field of rational numbers. The polynomial has four roots:

There are 24 possible ways to permute these four roots, but not all of these permutations are members of the Galois group. The members of the Galois group must preserve any algebraic equation with rational coefficients involving A, B, C and D. One such equation is

A + D = 0.

Therefore the permutation

(A, B, C, D) → (A, B, D, C)

is not permitted, because it transforms the valid equation A + D = 0 into the equation A + C = 0, which is invalid since .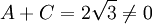

Another equation that the roots satisfy is

(A + B)² = 8.

This will exclude further permutations, such as

(A, B, C, D) → (A, C, B, D).

Continuing in this way, we find that the only permutations (satisfying both equations simultaneously) remaining are

(A, B, C, D) → (A, B, C, D)

(A, B, C, D) → (C, D, A, B)

(A, B, C, D) → (B, A, D, C)

(A, B, C, D) → (D, C, B, A),

and the Galois group is isomorphic to the Klein four-group.

The modern approach by field theory

In the modern approach, one starts with a field extension L/K, and examines the group of field automorphisms of L/K. See the article on Galois groups for further explanation and examples.

The connection between the two approaches is as follows. The coefficients of the polynomial in question should be chosen from the base field K. The top field L should be the field obtained by adjoining the roots of the polynomial in question to the base field. Any permutation of the roots which respects algebraic equations as described above gives rise to an automorphism of L/K, and vice versa.

In the first example above, we were studying the extension 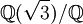, where Q is the field of rational numbers, and 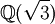is the field obtained from Q by adjoining 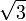. In the second example, we were studying the extension Q(A,B,C,D)/Q.

There are several advantages to the modern approach over the permutation group approach.

• It permits a far simpler statement of the fundamental theorem of Galois theory.
• The use of base fields other than Q is crucial in many areas of mathematics. For example, in algebraic number theory, one often does Galois theory using number fields, finite fields or local fields as the base field.
• It allows one to more easily study infinite extensions. Again this is important in algebraic number theory, where for example one often discusses the absolute Galois group of Q, defined to be the Galois group of K/Q where K is an algebraic closure of Q.
• It allows for consideration of inseparable extensions. This issue does not arise in the classical framework, since it was always implicitly assumed that arithmetic took place in characteristic zero, but nonzero characteristic arises frequently in number theory and in algebraic geometry.
• It removes the rather artificial reliance on chasing roots of polynomials. That is, different polynomials may yield the same extension fields, and the modern approach recognizes the connection between these polynomials.

Solvable groups and solution by radicals

The notion of a solvable group in group theory allows one to determine whether a polynomial is solvable in the radicals, depending on whether its Galois group has the property of solvability. In essence, each field extension L/K corresponds to a factor group in a composition series of the Galois group. If a factor group in the composition series is cyclic of order n, then the corresponding field extension is a radical extension, and the elements of L can then be expressed using the nth root of some element of K.

If all the factor groups in its composition series are cyclic, the Galois group is called solvable, and all of the elements of the corresponding field can be found by repeatedly taking roots, products, and sums of elements from the base field (usually Q).

One of the great triumphs of Galois Theory was the proof that for every n > 4, there exist polynomials of degree n which are not solvable by radicals—the Abel-Ruffini theorem. This is due to the fact that for n > 4 the symmetric group S_n contains a simple, non-cyclic, normal subgroup.

A non-solvable quintic example

Van der Waerden cites the polynomial f(x) = x⁵−x−1. By the rational root theorem it has no rational zeros. Neither does it have linear factors modulo 2 or 3.

f(x) has the factorization (x²+x+1)(x³+x²+1) modulo 2. That means its Galois group modulo 2 is cyclic of order 6.

f(x) has no quadratic factor modulo 3. Thus its Galois group modulo 3 has order 5.

A permutation group on 5 objects with operations of orders 6 and 5 must be the symmetric group S₅, which must be the Galois group of f(x). This is one of the simplest examples of a non-solvable quintic polynomial. Serge Lang said that Artin was fond of this example.

The inverse Galois problem

All finite groups do occur as Galois groups. It is easy to construct field extensions with any given finite group as Galois group, as long as one does not also specify the ground field.

For that, choose a field K and a finite group G. Cayley's theorem says that G is (up to isomorphism) a subgroup of the symmetric group S on the elements of G. Choose indeterminates {x_α}, one for each element α of G, and adjoin them to K to get the field F = K({x_α}). Contained within F is the field L of symmetric rational functions in the {x_α}. The Galois group of F/L is S, by a basic result of Emil Artin. G acts on F by restriction of action of S. If the fixed field of this action is M, then, by the fundamental theorem of Galois theory, the Galois group of F/M is G.

It is an open problem to prove the existence of a field extension of the rational field Q with a given finite group as Galois group. Hilbert played a part in solving the problem for all symmetric and alternating groups. Igor Shafarevich proved that every solvable finite group is the Galois group of some extension of Q. Various people have solved the inverse Galois problem for selected non-abelian simple groups. Existence of solutions has been shown for all but possibly one ( Mathieu group M₂₃) of the 26 sporadic simple groups. There is even a polynomial with integral coefficients whose Galois group is the Monster group.