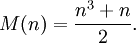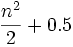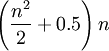Magic square
2008/9 Schools Wikipedia Selection. Related subjects: Mathematics
In recreational mathematics, a magic square of order n is an arrangement of n² numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n². The term "magic square" is also sometimes used to refer to any of various types of word square.
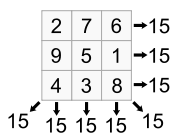
Normal magic squares exist for all orders n ≥ 1 except n = 2, although the case n = 1 is trivial—it consists of a single cell containing the number 1. The smallest nontrivial case, shown below, is of order 3.
The constant sum in every row, column and diagonal is called the magic constant or magic sum, M. The magic constant of a normal magic square depends only on n and has the value
For normal magic squares of order n = 3, 4, 5, …, the magic constants are:
- 15, 34, 65, 111, 175, 260, … (sequence A006003 in OEIS).
History of magic squares
The Lo Shu square (3×3 magic square)
Chinese literature dating from as early as 650 BC tells the legend of Lo Shu or "scroll of the river Lo". In ancient China, there was a huge flood. The people tried to offer some sacrifice to the river god of one of the flooding rivers, the Lo river, to calm his anger. Then, there emerged from the water a turtle with a curious figure/pattern on its shell; there were circular dots of numbers that were arranged in a three by three nine-grid pattern such that the sum of the numbers in each row, column and diagonal was the same: 15. This number is also equal to the number of days in each of the 24 cycles of the Chinese solar year. This pattern, in a certain way, was used by the people in controlling the river.
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
The Lo Shu Square, as the magic square on the turtle shell is called, is the unique normal magic square of order three in which 1 is at the bottom and 2 is in the upper right corner. Every normal magic square of order three is obtained from the Lo Shu by rotation or reflection.
The Square of Lo Shu is also referred to as the Magic Square of Saturn or Cronos. Its numerical value is obtained from the workings of the I Ching when the Trigrams are placed in an order given in the first river map, the Ho Tu or Yellow River. The Ho Tu produces 4 squares of Hexagrams 8 x 8 in its outer values of 1 to 6, 2 to 7, 3 to 8, and 4 to 9, and these outer squares can then be symmetrically added together to give an inner central square of 5 to 10. The central values of the Ho Tu are those of the Lo Shu (so they work together), since in the total value of 15 x 2 (light and dark) is found the number of years in the cycle of equinoctial precession (12,960 x 2 = 25,920). The Ho Tu produces a total of 40 light and 40 dark numbers called the days and nights (the alternations of light and dark), and a total of 8 x 8 x 8 Hexagrams whose opposite symmetrical addition equals 8640, therefore each value of a square is called a season as it equals 2160. 8640 is the number of hours in a 360-day year, and 2160 years equals an aeon (12 aeons = 25,920 yrs).
To validate the values contained in the 2 river maps (Ho Tu and Lo Shu) the I Ching provides numbers of Heaven and Earth that are the 'Original Trigrams' (father and mother) from 1 to 10. Heaven or a Trigram with all unbroken lines (light lines - yang) have odd numbers 1,3,5,7,9, and Earth a Trigram with all broken lines have even numbers 2,4,6,8,10. If each of the Trigram's lines is given a value by multiplying the numbers of Heaven and Earth, then the value of each line in Heaven 1 would be 1 + 2 + 3 = 6, and its partner in the Ho Tu of Earth 6 would be 6 + 12 + 18 = 36, these 2 'Original Trigrams' thereby produce 6 more Trigrams (or children in all their combinations) -- and when the sequences of Trigrams are placed at right angles to each other they produce an 8 x 8 square of Hexagrams (or cubes) that each have 6 lines of values. From this simple point the complex structure of the maths evolves as a hexadecimal progression, and it is the hexagon that is the link to the turtle or tortoise shell. In Chinese texts of the I Ching the moon is symbolic of water (darkness) whose transformations or changes create the light or fire - the dark value 6 creates the light when its number is increased by 1. This same principle can be found in ancient calendars such as the Egyptian, as the 360 day year of 8640 hrs was divided by 72 to produce the 5 extra days or 120 hours on which the gods were born. It takes 72 years for the heavens to move 1 degree through its Precession.
Cultural significance of magic squares
Magic squares have fascinated humanity throughout the ages, and have been around for over 4,000 years. They are found in a number of cultures, including Egypt and India, engraved on stone or metal and worn as talismans, the belief being that magic squares had astrological and divinatory qualities, their usage ensuring longevity and prevention of diseases.
The Kubera-Kolam is a floor painting used in India which is in the form of a magic square of order three. It is essentially the same as the Lo Shu Square, but with 19 added to each number, giving a magic constant of 72.
| 23 | 28 | 21 |
| 22 | 24 | 26 |
| 27 | 20 | 25 |
Arabia
Magic squares were known to Arabian mathematicians, possibly as early as the 7th century, when the Arabs got into contact with Indian or South Asian culture, and learned Indian mathematics and astronomy, including other aspects of combinatorial mathematics. It has also been suggested that the idea came via China. The first magic squares of order 5 and 6 appear in an encyclopedia from Baghdad circa 983 AD, the Rasa'il Ihkwan al-Safa (the Encyclopedia of the Brethern of Purity); simpler magic squares were known to several earlier Arab mathematicians.
The Arab mathematician Ahmad al-Buni, who worked on magic squares around 1200 A.D., attributed mystical properties to them, although no details of these supposed properties are known. There are also references to the use of magic squares in astrological calculations, a practice that seems to have originated with the Arabs.
India
A well known early magic square in India is found in Khajuraho in the Parshvanath Jain temple. It dates from 10th century .
| 7 | 12 | 1 | 14 |
| 2 | 13 | 8 | 11 |
| 16 | 3 | 10 | 5 |
| 9 | 6 | 15 | 4 |
This is referred to as the Chautisa Yantra, since each sub-square sums to 34.
Europe
In 1300, building on the work of the Arab Al-Buni, Greek Byzantine scholar Manuel Moschopoulos wrote a mathematical treatise on the subject of magic squares, leaving out the mysticism of his predecessors. Moschopoulos is thought to be the first Westerner to have written on the subject. In the 1450s the Italian Luca Pacioli studied magic squares and collected a large number of examples.
In about 1510 Heinrich Cornelius Agrippa wrote De Occulta Philosophia, drawing on the Hermetic and magical works of Marsilio Ficino and Pico della Mirandola, and in it he expounded on the magical virtues of seven magical squares of orders 3 to 9, each associated with one of the astrological planets. This book was very influential throughout Europe until the counter-reformation, and Agrippa's magic squares, sometimes called Kameas, continue to be used within modern ceremonial magic in much the same way as he first prescribed.
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The most common use for these Kameas is to provide a pattern upon which to construct the sigils of spirits, angels or demons; the letters of the entity's name are converted into numbers, and lines are traced through the pattern that these successive numbers make on the kamea. In a magical context, the term magic square is also applied to a variety of word squares or number squares found in magical grimoires, including some that do not follow any obvious pattern, and even those with differing numbers of rows and columns. They are generally intended for use as talismans. For instance the following squares are: The Sator square, one of the most famous magic squares found in a number of grimoires including the Key of Solomon; a square "to overcome envy", from The Book of Power; and two squares from The Book of the Sacred Magic of Abramelin the Mage, the first to cause the illusion of a superb palace to appear, and the second to be worn on the head of a child during an angelic invocation:
|
|
|
|
Albrecht Dürer's magic square
The order-4 magic square in Albrecht Dürer's engraving Melencolia I is believed to be the first seen in European art. It is very similar to Yang Hui's square, which was created in China about 250 years before Dürer's time. The sum 34 can be found in the rows, columns, diagonals, each of the quadrants, the centre four squares, the corner squares, the four outer numbers clockwise from the corners (3+8+14+9) and likewise the four counter-clockwise (the locations of four queens in the two solutions of the 4 queens puzzle ), the two sets of four symmetrical numbers (2+8+9+15 and 3+5+12+14) and the sum of the middle two entries of the two outer columns and rows (e.g. 5+9+8+12), as well as several kite-shaped quartets, e.g. 3+5+11+15; the two numbers in the middle of the bottom row give the date of the engraving: 1514. Dürer's Melencolia I plays a key role in The Art Thief, a novel by Noah Charney (Atria, 2007).
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
The Sagrada Família magic square
The Passion façade of the Sagrada Família church in Barcelona, designed by sculptor Josep Subirachs, features a 4×4 magic square:
The magic constant of the square is 33, the age of Jesus at the time of the Passion. Structurally, it is very similar to the Melancholia magic square, but it has had the numbers in four of the cells reduced by 1.
| 1 | 14 | 14 | 4 |
| 11 | 7 | 6 | 9 |
| 8 | 10 | 10 | 5 |
| 13 | 2 | 3 | 15 |
While having the same pattern of summation, this is not a normal magic square as above, as two numbers (10 and 14) are duplicated and two (12 and 16) are absent, failing the 1→n² rule.
Types of magic squares and their construction
There are many ways to construct magic squares, but the standard (and most simple) way is to follow certain configurations/formulas which generate regular patterns. Magic squares exist for all values of n, with only one exception - it is impossible to construct a magic square of order 2. Magic squares can be classified into three types: odd, doubly even (n divisible by four) and singly even (n even, but not divisible by four). Odd and doubly even magic squares are easy to generate; the construction of singly even magic squares is more difficult but several methods exist, including the LUX method for magic squares (due to John Horton Conway) and the Strachey method for magic squares.
Group theory was also used for constructing new magic squares of a given order from one of them, please see .
The number of different n×n magic squares for n from 1 to 5, not counting rotations and reflections:
- 1, 0, 1, 880, 275305224 (sequence A006052 in OEIS).
The number for n = 6 has been estimated to 1.7745×1019.
A method for constructing a magic square of odd order
Starting from the central column of the first row with the number 1, the fundamental movement for filling the squares is diagonally up and right, one step at a time. If a filled square is encountered, one moves vertically down one square instead, then continuing as before. When a move would leave the square, it is wrapped around to the last row or first column, respectively.
Similar patterns can also be obtained by starting from other squares.
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The following formulae help construct magic squares of odd order
|
||||||||||||
* Square roots are easier to calculate than cubic roots
Example:
|
||||||||||||
The "Middle Number" is always in the diagonal bottom left to top right.
The "Last Number" is always opposite the number 1 in an outside column or row.
A method of constructing a magic square of doubly even order
Doubly even means that n is an even multiple of an even integer; or 4p, where p is an integer. eg 4, 8, 12
Generic pattern
All the numbers are written in order from right to left across each row in turn, starting from the top left hand corner. Numbers are then either retained in the same place or interchanged with their diametrically opposite numbers in a certain regular pattern. In the magic square of order four, the numbers in the four central squares and one square at each corner are retained in the same place and the others are interchanged with their diametrically opposite numbers.
A construction of a magic square of order 4
Go left to right through the square filling counting and filling in on the diagonals only. Then continue by going left to right from the top left of the table and fill in counting down from 16 or n². As shown below.
|
|
||||||||||||||||||||||||||||||||||||||||
The medjig-method of constructing magic squares of even order n>4
This playful method is based on a 2006 published mathematical game called medjig (author: Willem Barink, editor: Philos-Spiele). The pieces of the medjig puzzle are squares divided in four quadrants on which the numbers 0, 1, 2 and 3 are dotted in all sequences. There are 18 squares, every sequence occurs 3 times. The aim of the puzzle is to take 9 squares out of the collection and arrange them in a 3 x 3 "medjig-square" in such a way that the series, columns and diagonals formed by the quadrants, show the sum of 9.
The medjig way of construction of a magic square of order 6 goes as follows. Arrange a 3 x 3 medjig square (for convenience this time you may choose unlimited from the whole collection). Then take the well-known classic 3 x 3 magic square and divide all fields of it in four quadrants. Next fill these quadrants with the original number and its three modulo-9 numbers up to 36, following the pattern of the medjig-solution. Doing so, the original field with the number 8 yields the four subfields with the numbers 8 (= 8 + 0x9), 17 (= 8 + 1x9), 26 (= 8 + 2x9) and 35 (= 8 + 3x9), the field with the number 3 yields the numbers 3, 12, 21 and 30, etc… See illustration below.
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The same way you can construct a magic square of order 8. You first have to construct a 4 x 4 medjig solution (sum of all series, columns and diagonals 12). And then enlarge e.g. the well-known Dürer 4 x 4 magic square modulo-16 to 64. For the construction of a magic square of order 10 you have to arrange a 5 x 5 medjig solution, for which two sets of medjig pieces are needed. For the order 12 you can simply duplicate horizontally and vertically a 3 x 3 medjig solution and then enlarge modulo-36 to 144 the order 6 magic square made above. Order 16 goes the same way.
The construction of panmagic squares
Any number p in the order-n square can be uniquely written in the form p = an + r, with r chosen from {1,...,n}. Note that due to this restriction, a and r are not the usual quotient and remainder of dividing p by n. Consequently the problem of constructing can be split in two problems easier to solve. So, construct two matching square grids of order n satisfying panmagic properties, one for the a-numbers (0,….,n-1), and one for the r-numbers (1,….,n). This requires a lot of puzzling, but can be done. When successful, combine them into one - panmagic - square. Van den Essen and many others supposed this was also the way the great Benjamin Franklin (1706-1790) constructed his famous franklin squares. Three panmagic squares are shown below. The first two squares have been constructed April 2007 by Barink, the third one is some years older, and comes from Donald Morris, who used, as he supposes, the franklin way of construction.
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The order 8 square satisfies all panmagic properties, including the franklin ones. It consists of 4 perfectly panmagic 4x4 units. Note that both order 12 squares show the property that any row or column can be divided in three parts having a sum of 290 (= 1/3 of the total sum of a row or column). This property compensates the absence of the more standard panmagic franklin property that any 1/2 row or column shows the sum of 1/2 of the total. For the rest the order 12 squares differ a lot.The Barink 12x12 square is composed of 9 perfectly panmagic 4x4 units, moreover any 4 consecutive numbers starting on any odd place in a row or column show a sum of 290. The Morris 12x12 square lacks these properties, but on the contrary shows constant franklindiagonals. For a better understanding of the constructing decompose the squares as described above, and see how it was done. And note the difference between the Barink constructions on the one hand, and the Morris/Franklin construction on the other hand.
In the book Mathematics in the Time-Life Science Library Series, magic squares by Euler and Franklin are shown. Franklin designed this one so that any four-square subset (any four contiguous squares that form a larger square, or any four squares equidistant from the centre) total 130. In Euler's square, the rows and columns each total 260, and halfway they total 130--and a chess knight, making its L-shaped moves on the square, can touch all 64 boxes in consecutive numerical order.
The construction of a magic square using genetic algorithms
A magic square can be constructed using genetic algorithms . This is an elegant trial and error process in which an initial population of magic squares with random values are generated. The fitnesses of these individual magic square are calculated based on the "flatness" of the magic square, that is, the degree of deviation in the sums of the rows, columns, and diagonals. The population of magic squares will interbreed (exchange values) in a manner coherent to genetics, based on the fitness score of the magic squares. Thus, magic squares with a higher fitness score will have a higher likelihood of reproducing. In the interbreeding process where the magic squares exchange their values, a mutation factor is introduced, imitating genetic mutation in nature. This mutation will be included or naturally excluded from the solution depending on their contribution to the fitness of the magic square. The next generation of the magic square population is again calculated for their fitness, and this process continues until a solution has been found.
Generalizations
Extra constraints
Certain extra restrictions can be imposed on magic squares. If not only the main diagonals but also the broken diagonals sum to the magic constant, the result is a panmagic square. If raising each number to certain powers yields another magic square, the result is a bimagic, a trimagic, or, in general, a multimagic square.
Different constraints
Sometimes the rules for magic squares are relaxed, so that only the rows and columns but not necessarily the diagonals sum to the magic constant. In heterosquares and antimagic squares, the 2n + 2 sums must all be different.
Other operations
Instead of adding the numbers in each row, column and diagonal, one can apply some other operation. For example, a multiplicative magic square has a constant product of numbers.
|
|
||||||||||||||||||||||||||||||||
Other magic shapes
Other shapes than squares can be considered, resulting, for example, in magic stars and magic hexagons. Going up in dimension results in magic cubes, magic tesseracts and other magic hypercubes.
Edward Shineman, an internationally renowned magic shape constructionist, has developed yet another design in the shape of magic diamonds. He has made many of these for commemorative and historical purposes, and has also experimented with other self-contained double rectangle/square combinations, L-shaped "lightening" figures, and more. The diamonds have been made in honour of events and people ranging from Tiger Woods to Ronald Reagan, from Cornell University anniversary's to special family birthdays. Several of his works have been featured in magic square books, as well as multiple publications in The Journal of Recreational Mathematics. An array of his magical contributions can be found at eds-magic-squares.com.
Combined extensions
One can combine two or more of the above extensions, resulting in such objects as multiplicative multimagic hypercubes. Little seems to be known about this subject.
Related problems
Over the years, many mathematicians, including Euler and Cayley have worked on magic squares, and discovered fascinating relations.
Magic square of primes
Rudolf Ondrejka (1928-2001) discovered the following 3x3 magic square of primes, in this case nine Chen primes:
| 17 | 89 | 71 |
| 113 | 59 | 5 |
| 47 | 29 | 101 |
The Green-Tao theorem implies that there are arbitrarily large magic squares consisting of primes.
n-Queens problem
In 1992, Demirörs, Rafraf, and Tanik published a method for converting some magic squares into N-queens solutions, and vice versa.
Date magic square
A date magic square is a 4×4 magic square in which the numbers in a given date (for example, April 15, 1707) are used to construct the first row (4, 15, 17, 07). The magic constant (M) of a 4×4 'normal' magic square is 34. If the four numbers in a date don't add up to 34, we cannot construct a 'normal' magic square for that date. In the above example, M=43:
| 4 | 15 | 17 | 07 |
| 5 | 19 | 13 | 6 |
| 20 | 9 | 2 | 12 |
| 14 | 0 | 11 | 18 |
The only difference between a magic square and a date magic square is that, in a date magic square repetition of numbers is not allowed in any row except the first one, whereas in a 'normal' magic square, repetition is not allowed in any row.
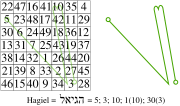
Number/Word Magic Square
A Number/Word combination magic square is constructed using the following three rules:
- Make a normal magic square of order 3 using any numbers.
- Count the number of letters in each number and replace the number with this count.
- The new square must also be magic.
An example of such a square is shown below:
|
|
|
||||||||||||||||||||||||||||||||||||
Tarry-Escott problem
By a strange coincidence, the 3×3 magic square contains a solution to the Tarry-Escott problem.
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
Prepare two number sets from the above magic square by combining numbers of last rows and last columns in the clockwise and anticlockwise directions:
- {492, 276, 618, 834}
- {294, 438, 816, 672}.
Tarry-Escott Solution:
- 4921 + 2761 + 6181 + 8341 = 2941 + 4381 + 8161 + 6721
- 4922 + 2762 + 6182 + 8342 = 2942 + 4382 + 8162 + 6722
- 4923 + 2763 + 6183 + 8343 = 2943 + 4383 + 8163 + 6723.
Magic Squares in contemporary literature
In Chapter 2 of The Great Brain is Back by John D. Fitzgerald, Tom, alias the "Great Brain", remembers having been told by a teacher about a magic square. After working on it for three days, he comes up with the Order 3, Sum 15 square. He then sets up the "numbers game", rounding up his friends and explaining the concept, charging 10 cents to play with a 50 cent prize for anyone who can solve it within two days, handing out a sheet with the 3*3 grid and the numbers one through nine to every player, and giving permission to all participants to get the help of their parents. Thinking it will be easy, all 20 kids present including his brother John (the narrator) opt to play and give him a dime. John shows it to their father, the only college graduate in town. His father explains that the first thing to do is to make a list of all the combinations of three numbers from 1 to 9 which total 15, excluding those in which one number is used more than once. Then (showing a lack of expertise on the subject) he says you have to "keep trying the different combinations until you get the right answer." John makes the list, and spends every free moment he has over the next two days trying to put the combinations together, without success. His father tells him to do it by elimination and start with the three squares in the middle, but does not elaborate. After two days, no one has solved it, and some believe that it can't be done. But when the deadline passes and there are no winners, Tom reveals the answer.
In Steve Martin's novel The Pleasure of My Company, the main character Daniel Pecan Cambridge builds magic squares as a way to relax.