Monte Carlo method

2008/9 Schools Wikipedia Selection. Related subjects: Mathematics

The Monte Carlo method can be illustrated as a game of battleship. First a player makes some random shots. Next the player applies algorithms (ie. a battleship is four dots in the vertical or horizontal direction). Finally based on the outcome of the random sampling and the algorithm the player can determine the likely locations of the other player's ships.

A Monte Carlo method is a computational algorithm that relies on repeated random sampling to compute its results. Monte Carlo methods are often used when simulating physical and mathematical systems. Because of their reliance on repeated computation and random or pseudo-random numbers, Monte Carlo methods are most suited to calculation by a computer. Monte Carlo methods tend to be used when it is infeasible or impossible to compute an exact result with a deterministic algorithm.

The term Monte Carlo was coined in the 1940s by physicists working on nuclear weapon projects in the Los Alamos National Laboratory.

Overview

There is no single Monte Carlo method; instead, the term describes a large and widely-used class of approaches. However, these approaches tend to follow a particular pattern:

1. Define a domain of possible inputs.
2. Generate inputs randomly from the domain, and perform a deterministic computation on them.
3. Aggregate the results of the individual computations into the final result.

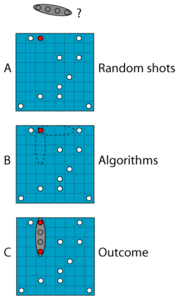
For example, the value of π can be approximated using a Monte Carlo method. Draw a square on the ground, then inscribe a circle within it. Now, scatter some small objects (for example, grains of rice or sand) throughout the square. If the objects are scattered uniformly, then the proportion of objects within the circle should be approximately π/4, which is the ratio of the circle's area to the square's area. Thus, if we count the number of objects in the circle, multiply by four, and divide by the number of objects in the square, we'll get an approximation of π.

Notice how the π approximation follows the general pattern of Monte Carlo algorithms. First, we define a domain of inputs: in this case, it's the square which circumscribes our circle. Next, we generate inputs randomly (scatter individual grains within the square), then perform a computation on each input (test whether it falls within the circle). At the end, we aggregate the results into our final result, the approximation of π. Note, also, two other common properties of Monte Carlo methods: the computation's reliance on good random numbers, and its slow convergence to a better approximation as more data points are sampled. If we just drop our grains in the centre of the circle, they might simply build up in a pile within the circle: they won't be uniformly distributed, and so our approximation will be way off. But if they are uniformly distributed, then the more grains we drop, the more accurate our approximation of π will become.

History

Monte Carlo methods were originally practiced under more generic names such as "statistical sampling". The name "Monte Carlo" was popularized by physics researchers Stanislaw Ulam, Enrico Fermi, John von Neumann, and Nicholas Metropolis, among others; the name is a reference to a famous casino in Monaco which Ulam's uncle would borrow money to gamble at. The use of randomness and the repetitive nature of the process are analogous to the activities conducted at a casino.

Random methods of computation and experimentation (generally considered forms of stochastic simulation) can be arguably traced back to the earliest pioneers of probability theory (see, e.g., Buffon's needle, and the work on small samples by William Gosset), but are more specifically traced to the pre-electronic computing era. The general difference usually described about a Monte Carlo form of simulation is that it systematically "inverts" the typical mode of simulation, treating deterministic problems by first finding a probabilistic analog. Previous methods of simulation and statistical sampling generally did the opposite: using simulation to test a previously understood deterministic problem. Though examples of an "inverted" approach do exist historically, they were not considered a general method until the popularity of the Monte Carlo method spread.

Perhaps the most famous early use was by Enrico Fermi in 1930, when he used a random method to calculate the properties of the newly-discovered neutron. Monte Carlo methods were central to the simulations required for the Manhattan Project, though were severely limited by the computational tools at the time. Therefore, it was only after electronic computers were first built (from 1945 on) that Monte Carlo methods began to be studied in depth. In the 1950s they were used at Los Alamos for early work relating to the development of the hydrogen bomb, and became popularized in the fields of physics, physical chemistry, and operations research. The Rand Corporation and the U.S. Air Force were two of the major organizations responsible for funding and disseminating information on Monte Carlo methods during this time, and they began to find a wide application in many different fields.

Uses of Monte Carlo methods require large amounts of random numbers, and it was their use that spurred the development of pseudorandom number generators, which were far quicker to use than the tables of random numbers which had been previously used for statistical sampling.

Applications

Monte Carlo simulation methods are especially useful in studying systems with a large number of coupled degrees of freedom, such as liquids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model). More broadly, Monte Carlo methods are useful for modeling phenomena with significant uncertainty in inputs, such as the calculation of risk in business (for its use in the insurance industry, see stochastic modelling). A classic use is for the evaluation of definite integrals, particularly multidimensional integrals with complicated boundary conditions.

Monte Carlo methods in finance are often used to calculate the value of companies, to evaluate investments in projects at corporate level or to evaluate financial derivatives. The Monte Carlo method is intended for financial analysts who want to construct stochastic or probabilistic financial models as opposed to the traditional static and deterministic models.

Monte Carlo methods are very important in computational physics, physical chemistry, and related applied fields, and have diverse applications from complicated quantum chromodynamics calculations to designing heat shields and aerodynamic forms.

Monte Carlo methods have also proven efficient in solving coupled integral differential equations of radiation fields and energy transport, and thus these methods have been used in global illumination computations which produce photorealistic images of virtual 3D models, with applications in video games, architecture, design, computer generated films, special effects in cinema, business, economics and other fields.

Monte Carlo methods are useful in many areas of computational mathematics, where a lucky choice can find the correct result. A classic example is Rabin's algorithm for primality testing: for any n which is not prime, a random x has at least a 75% chance of proving that n is not prime. Hence, if n is not prime, but x says that it might be, we have observed at most a 1-in-4 event. If 10 different random x say that "n is probably prime" when it is not, we have observed a one-in-a-million event. In general a Monte Carlo algorithm of this kind produces one correct answer with a guarantee n is composite, and x proves it so, but another one without, but with a guarantee of not getting this answer when it is wrong too often — in this case at most 25% of the time. See also Las Vegas algorithm for a related, but different, idea.

Application areas

Areas of application include:

• Graphics, particularly for ray tracing; a version of the Metropolis-Hastings algorithm is also used for ray tracing where it is known as Metropolis light transport
• Modeling light transport in biological tissue
• Monte Carlo methods in finance
• Reliability engineering
• In simulated annealing for protein structure prediction
• In semiconductor device research, to model the transport of current carriers
• Environmental science, dealing with contaminant behaviour
• Monte Carlo method in statistical physics; in particular, Monte Carlo molecular modeling as an alternative for computational molecular dynamics.
• Search And Rescue and Counter-Pollution. Models used to predict the drift of a life raft or movement of an oil slick at sea.
• In Probabilistic design for simulating and understanding the effects of variability
• In Physical chemistry, particularly for simulations involving atomic clusters
• In computer science
  • Las Vegas algorithm
  • LURCH
  • Computer Go
• Modeling the movement of impurity atoms (or ions) in plasmas in existing and tokamaks (e.g.: DIVIMP).
• In experimental particle physics, for designing detectors, understanding their behaviour and comparing experimental data to theory
• Nuclear and particle physics codes using the Monte Carlo method:
  • GEANT - CERN's simulation of high energy particles interacting with a detector.
  • CompHEP, PYTHIA - Monte-Carlo generators of particle collisions
  • MCNP(X) - LANL's radiation transport codes
  • EGS - Stanford's simulation code for coupled transport of electrons and photons
  • PEREGRINE - LLNL's Monte Carlo tool for radiation therapy dose calculations
  • BEAMnrc - Monte Carlo code system for modeling radiotherapy sources ( LINAC's)
  • PENELOPE - Monte Carlo for coupled transport of photons and electrons, with applications in radiotherapy
  • MONK - Serco Assurance's code for the calculation of k-effective of nuclear systems
  • Modelling of foam and cellular structures
  • Modeling of tissue morphogenesis

Other methods employing Monte Carlo

• Assorted random models, e.g. self-organised criticality
• Direct simulation Monte Carlo
• Dynamic Monte Carlo method
• Kinetic Monte Carlo
• Quantum Monte Carlo
• Quasi-Monte Carlo method using low-discrepancy sequences and self avoiding walks
• Semiconductor charge transport and the like
• Electron microscopy beam-sample interactions
• Stochastic optimization
• Cellular Potts model
• Markov chain Monte Carlo
• Cross-Entropy Method
• Applied information economics

Use in mathematics

In general, Monte Carlo methods are used in mathematics to solve various problems by generating suitable random numbers and observing that fraction of the numbers obeying some property or properties. The method is useful for obtaining numerical solutions to problems which are too complicated to solve analytically. The most common application of the Monte Carlo method is Monte Carlo integration.

Integration

Deterministic methods of numerical integration operate by taking a number of evenly spaced samples from a function. In general, this works very well for functions of one variable. However, for functions of vectors, deterministic quadrature methods can be very inefficient. To numerically integrate a function of a two-dimensional vector, equally spaced grid points over a two-dimensional surface are required. For instance a 10x10 grid requires 100 points. If the vector has 100 dimensions, the same spacing on the grid would require 10¹⁰⁰ points—far too many to be computed. 100 dimensions is by no means unreasonable, since in many physical problems, a "dimension" is equivalent to a degree of freedom. (See Curse of dimensionality.)

Monte Carlo methods provide a way out of this exponential time-increase. As long as the function in question is reasonably well-behaved, it can be estimated by randomly selecting points in 100-dimensional space, and taking some kind of average of the function values at these points. By the law of large numbers, this method will display 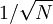convergence—i.e. quadrupling the number of sampled points will halve the error, regardless of the number of dimensions.

A refinement of this method is to somehow make the points random, but more likely to come from regions of high contribution to the integral than from regions of low contribution. In other words, the points should be drawn from a distribution similar in form to the integrand. Understandably, doing this precisely is just as difficult as solving the integral in the first place, but there are approximate methods available: from simply making up an integrable function thought to be similar, to one of the adaptive routines discussed in the topics listed below.

A similar approach involves using low-discrepancy sequences instead—the quasi-Monte Carlo method. Quasi-Monte Carlo methods can often be more efficient at numerical integration because the sequence "fills" the area better in a sense and samples more of the most important points that can make the simulation converge to the desired solution more quickly.

Integration methods

• Direct sampling methods
  • Importance sampling
  • Stratified sampling
  • Recursive stratified sampling
  • VEGAS algorithm
• Random walk Monte Carlo including Markov chains
  • Metropolis-Hastings algorithm
• Gibbs sampling

Optimization

Another powerful and very popular application for random numbers in numerical simulation is in numerical optimization. These problems use functions of some often large-dimensional vector that are to be minimized (or maximized). Many problems can be phrased in this way: for example a computer chess program could be seen as trying to find the optimal set of, say, 10 moves which produces the best evaluation function at the end. The traveling salesman problem is another optimization problem. There are also applications to engineering design, such as multidisciplinary design optimization.

Most Monte Carlo optimization methods are based on random walks. Essentially, the program will move around a marker in multi-dimensional space, tending to move in directions which lead to a lower function, but sometimes moving against the gradient.

Optimization methods

• Evolution strategy
• Genetic algorithms
• Parallel tempering
• Simulated annealing
• Stochastic optimization
• Stochastic tunneling

Inverse problems

Probabilistic formulation of inverse problems leads to the definition of a probability distribution in the model space. This probability distribution combines a priori information with new information obtained by measuring some observable parameters (data). As, in the general case, the theory linking data with model parameters is nonlinear, the a posteriori probability in the model space may not be easy to describe (it may be multimodal, some moments may not be defined, etc.).

When analyzing an inverse problem, obtaining a maximum likelihood model is usually not sufficient, as we normally also wish to have information on the resolution power of the data. In the general case we may have a large number of model parameters, and an inspection of the marginal probability densities of interest may be impractical, or even useless. But it is possible to pseudorandomly generate a large collection of models according to the posterior probability distribution and to analyze and display the models in such a way that information on the relative likelihoods of model properties is conveyed to the spectator. This can be accomplished by means of an efficient Monte Carlo method, even in cases where no explicit formula for the a priori distribution is available.

The best-known importance sampling method, the Metropolis algorithm, can be generalized, and this gives a method that allows analysis of (possibly highly nonlinear) inverse problems with complex a priori information and data with an arbitrary noise distribution. For details, see Mosegaard and Tarantola (1995) , or Tarantola (2005) .

Monte Carlo and random numbers

Interestingly, Monte Carlo simulation methods do not generally require truly random numbers to be useful - for other applications, such as primality testing, unpredictability is vital (see Davenport (1995)). Many of the most useful techniques use deterministic, pseudo-random sequences, making it easy to test and re-run simulations. The only quality usually necessary to make good simulations is for the pseudo-random sequence to appear "random enough" in a certain sense.

What this means depends on the application, but typically they should pass a series of statistical tests. Testing that the numbers are uniformly distributed or follow another desired distribution when a large enough number of elements of the sequence are considered is one of the simplest, and most common ones.

An alternative to the basic Monte Carlo method

Applied information economics (AIE) is a decision analysis method used in business and government that addresses some of the shortcomings of the Monte Carlo method - at least how it is usually employed in practical situations. The most important components AIE adds to the Monte Carlo method are:

1) Accounting for the systemic overconfidence of human estimators with calibrated probability assessment

2) Computing the economic value of information to guide additional empirical measurements

3) Using the results of Monte Carlos as input to portfolio analysis

When Monte Carlo simulations are used in most decision analysis settings, human experts are used to estimate the probabilities and ranges in the model. However, decision psychology research in the field of calibrated probability assessments shows that humans - especially experts in various fields - tend to be statistically overconfident. That is, they put too high a probability that a forecasted outcome will occur and they tend to use ranges that are too narrow to reflect their uncertainty. AIE involves training human estimators so that the probabilities and ranges they provide realistically reflect uncertainty (eg., a subjective 90% confidence interval as a 90% chance of containing the true value). Without such training, Monte Carlo models will invariably underestimate the uncertainty of a decision and therefore the risk.

Another shortcoming is that, in practice, most users of Monte Carlo simulations rely entirely on the initial subjective estimates and almost never follow up with empirical observation. This may be due to the overwhelming number of variables in many models and the inability of analysts to choose economically justified variables to measure further. AIE addresses this by using methods from decision theory to compute the economic value of additional information. This usually eliminates the need to measure most variables and puts pragmatic constraints on the methods used to measure those variables that have a significant information value.

The final shortcoming addressed by AIE is that the output of a Monte Carlo - at least for the analysis of business decisions - is simply the histogram of the resulting returns. No criteria is presented to determine if a particular distribution of results is acceptable or not. AIE uses Modern Portfolio Theory to determine which investments are desirable and what their relative priorities should be.