| Description |
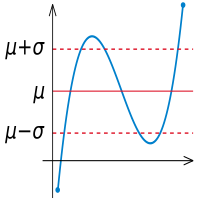
Illustration of en:Standard deviation |
| Source |
self-made with MATLAB. Tweaked in Inkscape |
| Date |
04:55, 4 August 2007 (UTC) |
| Author |
Oleg Alexandrov 04:55, 4 August 2007 (UTC) |
Permission
( Reusing this image) |
PD-self
|
|
|
I, the copyright holder of this work, hereby release it into the public domain. This applies worldwide.
In case this is not legally possible:
I grant anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law.
Afrikaans | Alemannisch | Aragonés | العربية | Asturianu | Български | Català | Cebuano | Česky | Cymraeg | Dansk | Deutsch | Eʋegbe | Ελληνικά | English | Español | Esperanto | Euskara | Estremeñu | فارسی | Français | Galego | 한국어 | हिन्दी | Hrvatski | Ido | Bahasa Indonesia | Íslenska | Italiano | עברית | Kurdî / كوردی | Latina | Lietuvių | Latviešu | Magyar | Македонски | Bahasa Melayu | Nederlands | Norsk (bokmål) | Norsk (nynorsk) | 日本語 | Polski | Português | Ripoarisch | Română | Русский | Shqip | Slovenčina | Slovenščina | Српски / Srpski | Suomi | Svenska | ไทย | Tagalog | Türkçe | Українська | Tiếng Việt | Walon | 中文(简体) | 中文(繁體) | zh-yue-hant | +/- |
MATLAB source code
% Illustartion of standard deviation
function main()
a=-1.2; b = 1.3;
c = -0.5; d = 2.5;
N=100;
X=linspace(a, b, N);
Y=X.^3-0.2*X.^2-X+2;
% Y=X.^2;
% scale Y to fit in the plotting window
Y = (Y-min(Y))/(max(Y)-min(Y));
Y = Y*(d-c)+c;
mean = sum(Y)/length(Y);
stdev = sqrt(sum((Y-mean).*(Y-mean))/length(Y));
figure(1); clf; hold on; axis off; axis equal;
lw = 3; % linewidth
lw2 = lw/2;
lw3 = lw/1.5;
fs = 30; % font size
red=[0.867 0.06 0.14];
blue = [0, 129, 205]/256;
green = [0, 200, 70]/256;
black = [0, 0, 0];
% plot the curves
shiftl=a-0.1;
small=0.2;
plot(X, Y, 'linewidth', lw, 'color', blue);
plot([shiftl max(X)+small], [mean, mean], 'linewidth', lw2, 'color', red);
plot([shiftl max(X)+small], [mean, mean]+stdev, 'linewidth', lw3, 'color', red, 'linestyle', '--');
plot([shiftl max(X)+small], [mean, mean]-stdev, 'linewidth', lw3, 'color', red, 'linestyle', '--');
% plot some balls for beauty
n = length(X);
ball_rad = 0.03;
ball(X(1), Y(1), ball_rad, blue)
ball(X(n), Y(n), ball_rad, blue)
% axes
small=0.2;
arrowsize=0.2; arrow_type=0;
angle=20; % in degrees
arrow([shiftl-0.2 0], [b+0.2, 0], lw2, arrowsize, angle, arrow_type, black)
arrow([shiftl, min(Y-0.1)], [shiftl, max(Y)], lw2, arrowsize, angle, arrow_type, black)
% text
small1 = 0.3; small2 = 0.3;
text(shiftl-small1, mean, '\mu', 'fontsize', fs)
text(shiftl-small1-small2, mean+stdev, '\mu+\sigma', 'fontsize', fs)
text(shiftl-small1-small2, mean-stdev, '\mu-\sigma', 'fontsize', fs)
% H=text(0.1, -0.1, 'x_{n+1}'); set(H, 'fontsize', fs)
% H=text(0.7, -0.1, 'x_{n}'); set(H, 'fontsize', fs)
% save to disk
saveas(gcf, 'Standard_deviation.eps', 'psc2')
% plot2svg('Standard_deviation.svg');
function arrow(start, stop, thickness, arrow_size, sharpness, arrow_type, color)
% Function arguments:
% start, stop: start and end coordinates of arrow, vectors of size 2
% thickness: thickness of arrow stick
% arrow_size: the size of the two sides of the angle in this picture ->
% sharpness: angle between the arrow stick and arrow side, in degrees
% arrow_type: 1 for filled arrow, otherwise the arrow will be just two segments
% color: arrow color, a vector of length three with values in [0, 1]
% convert to complex numbers
i=sqrt(-1);
start=start(1)+i*start(2); stop=stop(1)+i*stop(2);
rotate_angle=exp(i*pi*sharpness/180);
% points making up the arrow tip (besides the "stop" point)
point1 = stop - (arrow_size*rotate_angle)*(stop-start)/abs(stop-start);
point2 = stop - (arrow_size/rotate_angle)*(stop-start)/abs(stop-start);
if arrow_type==1 % filled arrow
% plot the stick, but not till the end, looks bad
t=0.5*arrow_size*cos(pi*sharpness/180)/abs(stop-start); stop1=t*start+(1-t)*stop;
plot(real([start, stop1]), imag([start, stop1]), 'LineWidth', thickness, 'Color', color);
% fill the arrow
H=fill(real([stop, point1, point2]), imag([stop, point1, point2]), color);
set(H, 'EdgeColor', 'none')
else % two-segment arrow
plot(real([start, stop]), imag([start, stop]), 'LineWidth', thickness, 'Color', color);
plot(real([stop, point1]), imag([stop, point1]), 'LineWidth', thickness, 'Color', color);
plot(real([stop, point2]), imag([stop, point2]), 'LineWidth', thickness, 'Color', color);
end
function ball(x, y, r, color)
Theta=0:0.1:2*pi;
X=r*cos(Theta)+x;
Y=r*sin(Theta)+y;
H=fill(X, Y, colour);
set(H, 'EdgeColor', 'none');
Click on a date/time to view the file as it appeared at that time.
The following pages on Schools Wikipedia link to this image (list may be incomplete):