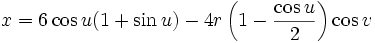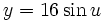From Wikipedia, the free encyclopedia
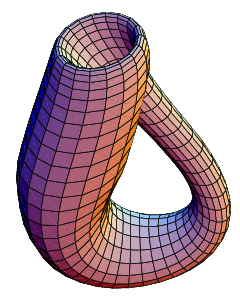 No higher resolution available.KleinBottle-01.png
No higher resolution available.KleinBottle-01.png (240 × 300 pixels, file size: 64 KB, MIME type: image/png)
 |
This is a file from the Wikimedia Commons. The description on its description page there is shown below.Commons is a freely licensed media file repository. You can help.
|
Summary
Standard immersion of a Klein bottle into R3. Made with Mathematica.
See also
Image:Klein bottle.svg
Licensing
|
|
I, the copyright holder of this work, hereby release it into the public domain. This applies worldwide.
In case this is not legally possible:
I grant anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law.
Afrikaans | Alemannisch | Aragonés | العربية | Asturianu | Български | Català | Cebuano | Česky | Cymraeg | Dansk | Deutsch | Eʋegbe | Ελληνικά | English | Español | Esperanto | Euskara | Estremeñu | فارسی | Français | Galego | 한국어 | हिन्दी | Hrvatski | Ido | Bahasa Indonesia | Íslenska | Italiano | עברית | Kurdî / كوردی | Latina | Lietuvių | Latviešu | Magyar | Македонски | Bahasa Melayu | Nederlands | Norsk (bokmål) | Norsk (nynorsk) | 日本語 | Polski | Português | Ripoarisch | Română | Русский | Shqip | Slovenčina | Slovenščina | Српски / Srpski | Suomi | Svenska | ไทย | Tagalog | Türkçe | Українська | Tiếng Việt | Walon | 中文(简体) | 中文(繁體) | zh-yue-hant | +/- |
Parameterization
This immersion of the Klein bottle into R3 is given by the following parameterization. Here the parameters u and v run from 0 to 2π and r is a fixed positive constant.
For 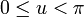 :
:
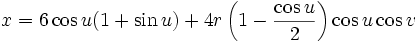
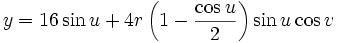
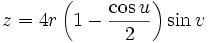
For 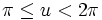 :
:
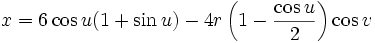
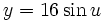
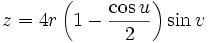
Mathematica source
KleinBottle[r_:1] =
Function[{u, v},
UnitStep[Sin[u]]
{
6 Cos[u](1 + Sin[u]) + 4r(1 - Cos[u]/2) Cos[u]Cos[v],
16 Sin[u] + 4r(1 - Cos[u]/2) Sin[u]Cos[v],
4r(1 - Cos[u]/2) Sin[v]
}
+ (1 - UnitStep[Sin[u]])
{
6 Cos[u](1 + Sin[u]) - 4r(1 - Cos[u]/2) Cos[v],
16 Sin[u],
4r(1 - Cos[u]/2) Sin[v]
}
]
ParametricPlot3D[Evaluate[KleinBottle[][u, v]], {u, 0, 2Pi}, {v, 0, 2Pi},
PlotPoints -> {50, 19}, Boxed -> False, Axes -> False,
ViewPoint -> {0.454, -2.439, -2.301}]
File history
Click on a date/time to view the file as it appeared at that time.
|
|
Date/Time |
Dimensions |
User |
Comment |
| current |
23:39, 12 December 2006 |
240×300 (64 KB) |
Mahahahaneapneap |
|
|
|
10:21, 15 September 2006 |
240×300 (77 KB) |
Dark knight |
|
|
|
02:23, 4 March 2005 |
240×300 (57 KB) |
Dbenbenn |
|
|
|
17:44, 3 March 2005 |
240×300 (71 KB) |
Fropuff |
|
File links
The following pages on Schools Wikipedia link to this image (list may be incomplete):
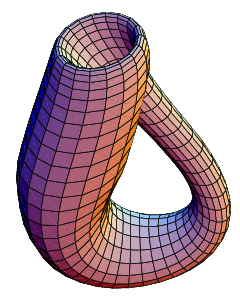

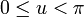 :
: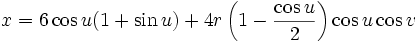
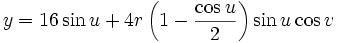
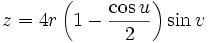
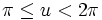 :
: