Arabic numerals
2008/9 Schools Wikipedia Selection. Related subjects: Mathematics
| Numeral systems by culture | |
|---|---|
| Hindu-Arabic numerals | |
| Indian Eastern Arabic Khmer |
Indian family Brahmi Thai |
| East Asian numerals | |
| Chinese Suzhou Counting rods |
Japanese Korean |
| Alphabetic numerals | |
| Abjad Armenian Cyrillic Ge'ez |
Hebrew Greek (Ionian) Āryabhaṭa |
| Other systems | |
| Attic Babylonian Egyptian Etruscan |
Mayan Roman Urnfield |
| List of numeral system topics | |
| Positional systems by base | |
| Decimal (10) | |
| 2, 4, 8, 16, 32, 64 | |
| 1, 3, 9, 12, 20, 24, 30, 36, 60, more… | |
Arabic numerals are the traditional name for the digits invented by Indian mathematicians in around AD 500 and the system by which a sequence of digits (e.g. "436") represents a number. The reason that they are known as Arabic rather than Indian numerals owes to how Arabic speakers conveyed the system from India to Europe during the Middle Ages, leading Europeans to attribute the numerals to the Arabic language. They are the most common symbolic representation of numbers around the world and are considered an important milestone in the development of mathematics.
One may distinguish between the decimal system involved, also known as the Hindu-Arabic numeral system, and the precise glyphs used. The glyphs most commonly used in conjunction with the Latin alphabet since Early Modern times are 0 1 2 3 4 5 6 7 8 9.
They were transmitted first to West Asia, where they find mention in the 9th century, and eventually to Europe in the 10th century. Since knowledge of the numerals reached Europe through the work of Arab mathematicians and astronomers, the numerals came to be called "Arabic numerals."
One also distinguishes an eastern arabic form of these numerals and a western arabic form, closer to the modern western, worldwide form.
History
Origins
The symbols for 1 to 9 in the Hindu-Arabic numeral system evolved from the Brahmi numerals. Buddhist inscriptions from around 300 BC use the symbols which became 1, 4 and 6. One century later, their use of the symbols which became 2, 7 and 9 was recorded.
The first universally accepted inscription containing the use of the 0 glyph is first recorded in the 9th century, in an inscription at Gwalior dated to 870. However, by this time, the use of the glyph had already reached Persia, and is mentioned in Al-Khwarizmi's descriptions of Indian numerals. Indian documents on copper plates, with the same symbol for zero in them, dated back as far as the 6th century AD, abound.
The numeral system came to be known to both the Persian mathematician Al-Khwarizmi, whose book On the Calculation with Hindu Numerals written about 825, and the Arab mathematician Al-Kindi, who wrote four volumes, "On the Use of the Indian Numerals" (Ketab fi Isti'mal al-'Adad al-Hindi) about 830, are principally responsible for the diffusion of the Indian system of numeration in the Middle East and the West. In the 10th century, Middle-Eastern mathematicians extended the decimal numeral system to include fractions, as recorded in a treatise by Syrian mathematician Abu'l-Hasan al-Uqlidisi in 952–53.
In the Arab world—until modern times—the Arabic numeral system was used only by mathematicians. Muslim scientists used the Babylonian numeral system, and merchants used the Abjad numerals. It was not until Fibonacci that the Arabic numeral system was used by a large population.
A distinctive West Arabic variant of the symbols begins to emerge around the 10th century in the Maghreb and Al-Andalus, called ghubar ("sand-table" or "dust-table") numerals.
The first mentions of the numerals in the West are found in the Codex Vigilanus of 976 . From the 980s, Gerbert of Aurillac (later, Pope Silvester II) began to spread knowledge of the numerals in Europe. Gerbert studied in Barcelona in his youth, and he is known to have requested mathematical treatises concerning the astrolabe from Lupitus of Barcelona after he had returned to France.
Adoption in Europe

In 825 Al-Khwārizmī, the Persian scientist, wrote a treatise, On the Calculation with Hindu Numerals, which was translated into Latin in the 12th century as Algoritmi de numero Indorum, where Algoritmi, the translator's rendition of the author's name, gave rise to the word algorithm (Latin algorithmus, "calculation method").
Fibonacci, an Italian mathematician who had studied in Bejaia ( Bougie), Algeria, promoted the Arabic numeral system in Europe with his book Liber Abaci, which was written in 1202, still describing the numerals as Indian rather than Arabic.
- "When my father, who had been appointed by his country as public notary in the customs at Bugia acting for the Pisan merchants going there, was in charge, he summoned me to him while I was still a child, and having an eye to usefulness and future convenience, desired me to stay there and receive instruction in the school of accounting. There, when I had been introduced to the art of the Indians' nine symbols through remarkable teaching, knowledge of the art very soon pleased me above all else and I came to understand it.."
The numerals are arranged with their lowest value digit to the right, with higher value positions added to the left. This arrangement was adopted identically into the numerals as used in Europe. The Latin alphabet running from left to right, unlike the Arabic alphabet, this resulted in an inverse arrangement of the place-values relative to the direction of reading.
The European acceptance of the numerals was accelerated by the invention of the printing press, and they became commonly known during the 15th century. Early uses in England include a 1445 inscription on the tower of Heathfield Church, Sussex, a 1448 inscription on a wooden lych-gate of Bray Church, Berkshire, and a 1487 inscription on the belfry door at Piddletrenthide church, Dorset and in Scotland a 1470 inscription on the tomb of the first Earl of Huntly in Elgin, ( Elgin, Moray) Cathedral. (See G.F. Hill, The Development of Arabic Numerals in Europe for more examples.) By the mid-16th century, they were in common use in most of Europe. Roman numerals remained in use mostly for the notation of Anno Domini years, and for numbers on clockfaces. Sometimes, Roman numerals are still used for enumeration of lists (as an alternative to alphabetical enumeration), and numbering pages in prefatory material in books.
Evolution of symbols
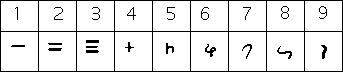
The numeral system employed, known as algorism, is positional decimal notation. Various symbol sets are used to represent numbers in the Arabic numeral system, all of which evolved from the Brahmi numerals. The symbols used to represent the system have split into various typographical variants since the Middle Ages:
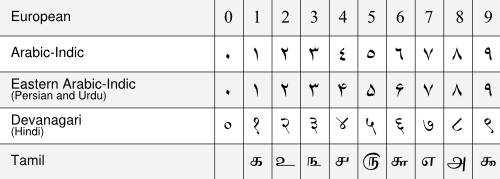
- The widespread Western Arabic numerals used with the Latin alphabet, in the table below labelled European, descended from the West Arabic numerals developed in al-Andalus and the Maghreb. (There are two typographic styles for rendering European numerals, known as lining figures and text figures).
- The Arabic-Indic or Eastern Arabic numerals used with the Arabic alphabet developed primarily in what is now Iraq. A variant of the Eastern Arabic numerals used in the Persian and Urdu languages is shown as East Arabic-Indic.
- The Devanagari numerals used with Devanagari and related variants are grouped as Indian numerals.
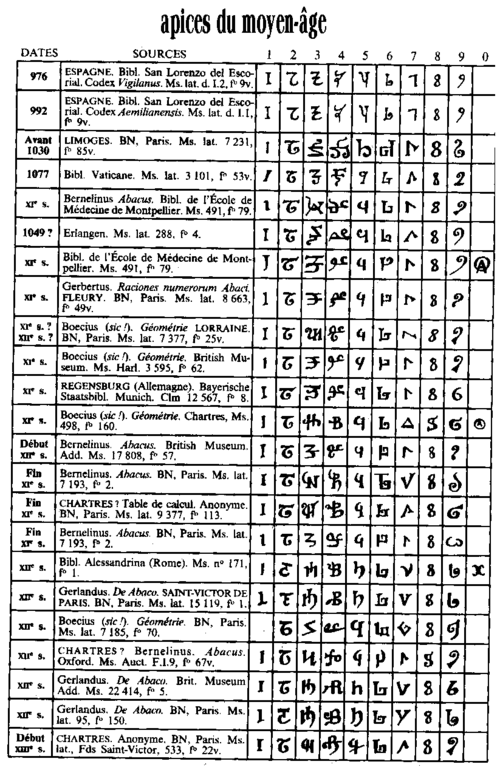
The evolution of the numerals in early Europe is shown on a table created by the French scholar J.E. Montucla in his Histoire de la Mathematique, which was published in 1757:
The Arabic numerals are encoded in ASCII (and Unicode) at positions 48 to 57:
| Binary | Dec | Hex | Glyph |
|---|---|---|---|
| 0011 0000 | 48 | 30 | 0 |
| 0011 0001 | 49 | 31 | 1 |
| 0011 0010 | 50 | 32 | 2 |
| 0011 0011 | 51 | 33 | 3 |
| 0011 0100 | 52 | 34 | 4 |
| 0011 0101 | 53 | 35 | 5 |
| 0011 0110 | 54 | 36 | 6 |
| 0011 0111 | 55 | 37 | 7 |
| 0011 1000 | 56 | 38 | 8 |
| 0011 1001 | 57 | 39 | 9 |