Euler characteristic
2008/9 Schools Wikipedia Selection. Related subjects: Mathematics
In algebraic topology, the Euler characteristic is a topological invariant, a number that describes one aspect of a topological space's shape or structure. It is commonly denoted by χ (Greek letter chi).
The Euler characteristic was originally defined for polyhedra and used to prove various theorems about them, including the classification of the Platonic solids. Leonhard Euler, for whom the concept is named, was responsible for much of this early work. In modern mathematics, the Euler characteristic arises from homology and connects to many other invariants.
Polyhedra
The Euler characteristic χ was classically defined for polyhedra, according to the formula
where V, E, and F are respectively the numbers of vertices (corners), edges and faces in the given polyhedron. A convex polyhedron is homeomorphic to a sphere, so its Euler characteristic is
This result is known as Euler's formula, and can be applied not only to polyhedra but also to embedded planar graphs. A proof is given below.
Examples of convex polyhedra
| Name | Image | Vertices V |
Edges E |
Faces F |
Euler characteristic: V − E + F |
|---|---|---|---|---|---|
| Tetrahedron | 4 | 6 | 4 | 2 | |
| Hexahedron or cube |  |
8 | 12 | 6 | 2 |
| Octahedron |  |
6 | 12 | 8 | 2 |
| Dodecahedron |  |
20 | 30 | 12 | 2 |
| Icosahedron | 12 | 30 | 20 | 2 |
Proof of Euler's formula
The first rigorous proof of Euler's formula, given by a 20-year-old Cauchy, is as follows.
Remove one face of the polyhedron. By pulling the edges of the missing face away from each other, deform all the rest into a planar network of points and curves, as illustrated by the first of the three graphs for the special case of the cube. (The assumption that the polyhedron is homeomorphic to the sphere at the beginning is what makes this possible.) After this deformation, the regular faces are generally not regular anymore—in fact, they are not even polygons. The number of vertices and edges has remained the same, but the number of faces has been reduced by 1. As such, proving Euler's formula for the polyhedron reduces to proving V − E + F =1 for this deformed, planar object.
If there is a face with more than three sides, draw a diagonal—that is, a curve through the face connecting two vertices that aren't connected yet. This adds one edge and one face and does not change the number of vertices, so it does not change the quantity V − E + F. Continue adding edges in this manner until all of the faces are triangular.
Apply repeatedly either of the following two transformations:
- Remove a triangle with only one edge adjacent to the exterior, as illustrated by the second graph. This decreases the number of edges and faces by one each and does not change the number of vertices, so it preserves V − E + F.
- Remove a triangle with two edges shared by the exterior of the network, as illustrated by the third graph. Each triangle removal removes a vertex, two edges and one face, so it preserves V − E + F.
Repeat these two steps, one after the other, until only one triangle remains.
At this point the lone triangle has V = 3, E = 3, and F = 1, so that V − E + F = 1. Since each of the two above transformation steps preserved this quantity, we have shown V − E + F = 1 for the deformed, planar object thus demonstrating V − E + F = 2 for the polyhedron. This proves the theorem.
For additional proofs, see Nineteen Proofs of Euler's Formula by David Eppstein. Multiple proofs, including their flaws and limitations, are used as examples in Proofs and Refutations by Imre Lakatos
Examples of non-convex polyhedra
Nonconvex polyhedra can have various Euler characteristics:
| Name | Image | Vertices V |
Edges E |
Faces F |
Euler characteristic: V − E + F |
|---|---|---|---|---|---|
| Tetrahemihexahedron |  |
6 | 12 | 7 | 1 |
| Octahemioctahedron |  |
12 | 24 | 12 | 0 |
| Cubohemioctahedron |  |
12 | 24 | 10 | −2 |
Formal definition
The polyhedra discussed above are, in modern language, two-dimensional finite CW-complexes. (When only triangular faces are used, they are two-dimensional finite simplicial complexes.) In general, for any finite CW-complex, the Euler characteristic can be defined as the alternating sum
where kn denotes the number of cells of dimension n in the complex.
More generally still, for any topological space, we can define the nth Betti number bn as the rank of the n-th homology group. The Euler characteristic can then be defined as the alternating sum
This quantity is well-defined if the Betti numbers are all finite and if they are zero beyond a certain index n0. This definition subsumes the previous ones.
Another generalization of the classical Euler characteristic—used in algebraic geometry—is as follows: for any sheaf  on a projective scheme X, one defines its Euler characteristic
on a projective scheme X, one defines its Euler characteristic  , where
, where  is the dimension of the ith sheaf cohomology group of
is the dimension of the ith sheaf cohomology group of  .
.
Properties
Homotopy invariance
Since the homology is a topological invariant (in fact, a homotopy invariant — two topological spaces that are homotopy equivalent have isomorphic homology groups), so is the Euler characteristic.
Inclusion-exclusion principle
If M and N are any two topological spaces, then the Euler characteristic of their disjoint union is the sum of their Euler characteristics, since homology is additive under disjoint union:
More generally, if M and N are subspaces of a larger space X, then so are their union and intersection. In some cases, the Euler characteristic obeys a version of the inclusion-exclusion principle:
This is true in the following cases:
- if M and N are an excisive couple. In particular, if the interiors of M and N inside the union still cover the union.
- if X is a locally compact space, and one uses Euler characteristics with compact supports, no assumptions on M or N are needed.
- if X is a stratified space all of whose strata are even dimensional, the inclusion-exclusion principle holds if M and N are unions of strata. This applies in particular if M and N are subvarieties of a complex algebraic variety.
In general, the inclusion-exclusion principle is false. A counterexample is given by taking X to be the real line, M a subset consisting of one point and N the complement of M.
Product property
Also, the Euler characteristic of any product space M × N is
These addition and multiplication properties are also enjoyed by cardinality of sets. In this way, the Euler characteristic can be viewed as a generalisation of cardinality; see .
Other properties
As a corollary of Poincaré duality, the Euler characteristic of any closed odd-dimensional manifold is zero. This applies more generally to any compact stratified space all of whose strata are odd-dimensional.
Relations to other invariants
The Euler characteristic of a closed orientable surface can be calculated from its genus g (the number of tori in a connected sum decomposition of the surface; intuitively, the number of "handles") as
- χ = 2 − 2g.
The Euler characteristic of a closed non-orientable surface can be calculated from its non-orientable genus k (the number of real projective planes in a connected sum decomposition of the surface) as
- χ = 2 − k.
For closed smooth manifolds, the Euler characteristic coincides with the Euler number, i.e., the Euler class of its tangent bundle evaluated on the fundamental class of a manifold. The Euler class, in turn, relates to all other characteristic classes of vector bundles.
For closed Riemannian manifolds, the Euler characteristic can also be found by integrating the curvature; see the Gauss-Bonnet theorem for the two-dimensional case and the generalized Gauss-Bonnet theorem for the general case.
A discrete analog of the Gauss-Bonnet theorem is Descartes' theorem that the "total defect" of a polyhedron, measured in full circles, is the Euler characteristic of the polyhedron; see defect (geometry).
Hadwiger's theorem characterizes the Euler characteristic as the unique ( up to scalar multiplication) translation-invariant, finitely additive, not-necessarily-nonnegative set function defined on finite unions of compact convex sets in Rn that is "homogeneous of degree 0".
Examples
Any contractible space (that is, one homotopy equivalent to a point) has trivial homology, meaning that the 0th Betti number is 1 and the others 0. Therefore its Euler characteristic is 1. This case includes Euclidean space 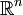 of any dimension, as well as the solid unit ball in any Euclidean space — the one-dimensional interval, the two-dimensional disk, the three-dimensional ball, etc.
of any dimension, as well as the solid unit ball in any Euclidean space — the one-dimensional interval, the two-dimensional disk, the three-dimensional ball, etc.
The Euler characteristic can be calculated easily for general surfaces by finding a polygonization of the surface (that is, a description as a CW-complex) and using the above definitions.
| Name | Image | Euler characteristic |
|---|---|---|
| Sphere |  |
2 |
| Torus |  |
0 |
| Double torus |  |
-2 |
| Triple torus |  |
-4 |
| Real projective plane |  |
1 |
| Möbius strip |  |
0 |
| Klein bottle |  |
0 |
| Two spheres (not connected) |   |
2 + 2 = 4 |
Partially ordered sets
The concept of Euler characteristic of a bounded finite poset is another generalization, important in combinatorics. A poset is "bounded" if it has smallest and largest elements; let us call them 0 and 1. The Euler characteristic of such a poset is defined as μ(0,1), where μ is the Möbius function in that poset's incidence algebra.







